设函数 ,其中
,其中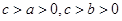 .
.
(1)记集合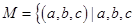 不能构成一个三角形的三边长,且
不能构成一个三角形的三边长,且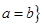 ,则
,则 所对应的
所对应的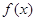 的零点的取值集合为 ;
的零点的取值集合为 ;
(2)若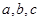 是
是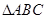 的三边长,则下列结论正确的是 (写出所有正确结论的序号).
的三边长,则下列结论正确的是 (写出所有正确结论的序号).
①对于区间 内的任意
内的任意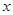 ,总有
,总有 成立;
成立;
②存在实数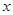 ,使得
,使得 不能同时成为任意一个三角形的三条边长;
不能同时成为任意一个三角形的三条边长;
③若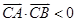 ,则存在实数
,则存在实数 ,使
,使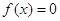 .(提示 :
.(提示 : )
)
(第(1)空2分,第(2)空3分)
相关知识点
推荐套卷
设函数 ,其中
,其中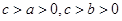 .
.
(1)记集合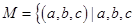 不能构成一个三角形的三边长,且
不能构成一个三角形的三边长,且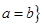 ,则
,则 所对应的
所对应的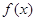 的零点的取值集合为 ;
的零点的取值集合为 ;
(2)若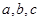 是
是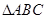 的三边长,则下列结论正确的是 (写出所有正确结论的序号).
的三边长,则下列结论正确的是 (写出所有正确结论的序号).
①对于区间 内的任意
内的任意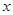 ,总有
,总有 成立;
成立;
②存在实数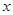 ,使得
,使得 不能同时成为任意一个三角形的三条边长;
不能同时成为任意一个三角形的三条边长;
③若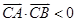 ,则存在实数
,则存在实数 ,使
,使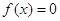 .(提示 :
.(提示 : )
)
(第(1)空2分,第(2)空3分)