某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有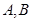 两个定点投篮位置,在
两个定点投篮位置,在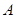 点投中一球得2分,在
点投中一球得2分,在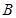 点投中一球得3分。某规则是:按先
点投中一球得3分。某规则是:按先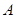 后
后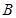 再
再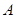 的顺序投篮,教师甲在
的顺序投篮,教师甲在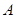 和
和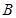 点投中的概率分别是
点投中的概率分别是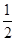 和
和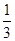 ,且在
,且在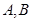 两点投中与否相互独立。
两点投中与否相互独立。
(1)若教师甲投篮三次,试求他投篮得分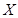 的分布列和数学期望;
的分布列和数学期望;
(2)若教师乙与教师甲在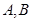 投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
推荐套卷
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有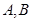 两个定点投篮位置,在
两个定点投篮位置,在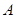 点投中一球得2分,在
点投中一球得2分,在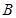 点投中一球得3分。某规则是:按先
点投中一球得3分。某规则是:按先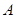 后
后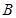 再
再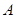 的顺序投篮,教师甲在
的顺序投篮,教师甲在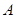 和
和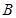 点投中的概率分别是
点投中的概率分别是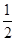 和
和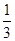 ,且在
,且在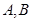 两点投中与否相互独立。
两点投中与否相互独立。
(1)若教师甲投篮三次,试求他投篮得分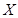 的分布列和数学期望;
的分布列和数学期望;
(2)若教师乙与教师甲在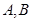 投中的概率相同,两人按规则各投三次,求甲胜乙的概率。
投中的概率相同,两人按规则各投三次,求甲胜乙的概率。