△ABC是锐角三角形,BC=6,面积为12.点P在AB上,点Q在AC上.如图9-33,正方形PQRS(RS与A在PQ的异侧)的边长为x,正方形PQRS与△ABC的公共部分的面积为y.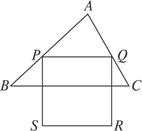
(1)当RS落在BC上时,求x;
(2)当RS不落在BC上时,求y与x的函数关系式;
(3)求公共部分面积的最大值.
相关知识点
推荐套卷
△ABC是锐角三角形,BC=6,面积为12.点P在AB上,点Q在AC上.如图9-33,正方形PQRS(RS与A在PQ的异侧)的边长为x,正方形PQRS与△ABC的公共部分的面积为y.
(1)当RS落在BC上时,求x;
(2)当RS不落在BC上时,求y与x的函数关系式;
(3)求公共部分面积的最大值.