如图,已知抛物线C1:x2+by=b2经过椭圆C2: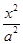
+
=1(a>b>0)的两个焦点.
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
，椭圆的离心率
短轴长为2，0为坐标原点.相关知识点
推荐套卷
如图,已知抛物线C1:x2+by=b2经过椭圆C2: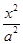+=1(a>b>0)的两个焦点.
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
粤公网安备 44130202000953号