下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
相关知识点
推荐套卷
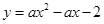 经过点B。
经过点B。
 (亩)与补贴数额
(亩)与补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额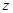 (元)会相应降低,且
(元)会相应降低,且
 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额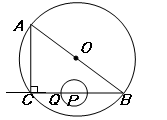
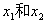
 ,求k的值.
,求k的值.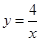 的图象上的概率;
的图象上的概率;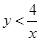 的概率.
的概率. 粤公网安备 44130202000953号
粤公网安备 44130202000953号