设椭圆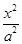
+
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y-
)2=16相交于M,N两点,且|MN|=
|AB|,求椭圆的方程.
相关试题
(x∈R)，试确定a的值，使f(x)为奇函数；
)．
；
；
；
.推荐套卷
设椭圆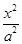+=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y-)2=16相交于M,N两点,且|MN|=|AB|,求椭圆的方程.
粤公网安备 44130202000953号