已知圆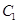 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线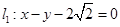 相切.
相切.
(1)求圆的标准方程;
(2)设点A为圆上一动点,AN
 轴于N,若动点Q满足
轴于N,若动点Q满足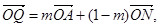 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点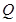 的轨迹方程
的轨迹方程 .
.
(3)在(2)的结论下,当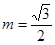 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与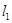 垂直的直线
垂直的直线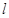 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求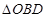 面积的最大值.
面积的最大值.
推荐套卷
已知圆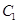 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线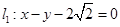 相切.
相切.
(1)求圆的标准方程;
(2)设点A为圆上一动点,AN
 轴于N,若动点Q满足
轴于N,若动点Q满足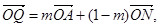 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点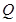 的轨迹方程
的轨迹方程 .
.
(3)在(2)的结论下,当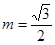 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与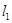 垂直的直线
垂直的直线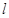 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求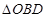 面积的最大值.
面积的最大值.