设平面向量a=(cosx,sinx),b=(cosx+2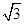 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0, ),证明:a和b不平行;
),证明:a和b不平行;
(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.
相关知识点
推荐套卷
设平面向量a=(cosx,sinx),b=(cosx+2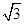 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0, ),证明:a和b不平行;
),证明:a和b不平行;
(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.