如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm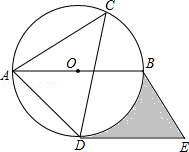
（1）请判断DE与⊙O的位置关系，并说明理由；
（2）求图中阴影部分的面积（结果用π表示）．
，并求a=2时代数式的值．
；
与
成反比例，并且当
时
。
之间的函数解析式；
、
、
在不在这个函数的图象上？
相关知识点
推荐套卷
如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm
（1）请判断DE与⊙O的位置关系，并说明理由；
（2）求图中阴影部分的面积（结果用π表示）．
粤公网安备 44130202000953号