如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P
ACB的大小为60°.过P作PH⊥EF于H.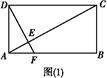
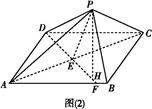
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P
ABC体积的最大值.
相关试题
有两个不等的负根，q:方程
无实根，若p或q为真，p且q为假，求m的取值范围。
定圆
动圆M与定圆
都外切，求动圆圆心M的轨迹方程。
，若非p是q的充分不必要条件，求a的取值范围。
的椭圆的标准方程
，求椭圆方程。
。
的奇偶性；相关知识点
推荐套卷
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角PACB的大小为60°.过P作PH⊥EF于H.
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体PABC体积的最大值.
粤公网安备 44130202000953号