已知函数f(x)＝lnx－ax2＋(2－a)x.
(1)讨论f(x)的单调性；
(2)设a>0，证明：当0<x<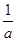
时，f
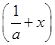>f
；
(3)若函数y＝f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：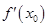
＜0.
，
．
，求数列
的前n项和
．
，
，
，且
．
，
，求
的解集．
，
，若
与
的夹角为
，求(1)
（2）求
的前
项和为
，且
.
是等比数列；
的通项公式，并求出使得
成立的最小正整数相关知识点
推荐套卷
已知函数f(x)＝lnx－ax2＋(2－a)x.
(1)讨论f(x)的单调性；
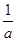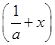(2)设a>0，证明：当0<x<时，f>f；
(3)若函数y＝f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明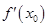：＜0.
粤公网安备 44130202000953号