某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设，阴影部分为一公共设施建设不能开发，且要求用栏栅隔开(栏栅要求在一直线上)，公共设施边界为曲线f(x)＝1－ax2(a＞0)的一部分，栏栅与矩形区域的边界交于点M、N，交曲线于点P，设P(t，f(t))．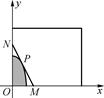
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t)；
(2)若在t＝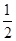
处，S(t)取得最小值，求此时a的值及S(t)的最小值．
中，角
、
、
的对边分别为
，且满足
，
、求角
、若
求
的不等式
，
时，解上述不等式；
的取值范围。
的不等式
。
中，
，
中，
，求数列
项和
。
中，已知
，
，
， 求
、
及
。推荐套卷
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设，阴影部分为一公共设施建设不能开发，且要求用栏栅隔开(栏栅要求在一直线上)，公共设施边界为曲线f(x)＝1－ax2(a＞0)的一部分，栏栅与矩形区域的边界交于点M、N，交曲线于点P，设P(t，f(t))．
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t)；
(2)若在t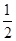＝处，S(t)取得最小值，求此时a的值及S(t)的最小值．
粤公网安备 44130202000953号