修建一个面积为
平方米的矩形场地的围墙，要求在前面墙的正中间留一个宽度为2米的出入口，后面墙长度不超过20米.已知后面墙的造价为每米45元，其他墙的造价为每米180元，设后面墙长度为
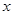米，修建此矩形场地围墙的总费用为
元.
（1）求的表达式；
（2）试确定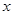，使修建此矩形场地围墙的总费用最小，并求出最小总费用.
，定义函数
最小正周期；
，求边AC的长．
中，
，
，求
.
的最大值.
中，
，
，
，求数列
是等差数列的前n项的和
.
中，
.
的值.推荐套卷
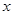修建一个面积为平方米的矩形场地的围墙，要求在前面墙的正中间留一个宽度为2米的出入口，后面墙长度不超过20米.已知后面墙的造价为每米45元，其他墙的造价为每米180元，设后面墙长度为米，修建此矩形场地围墙的总费用为元.
（1）求的表达式；
（2）试确定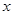，使修建此矩形场地围墙的总费用最小，并求出最小总费用.
粤公网安备 44130202000953号