设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
相关知识点
推荐套卷
 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点 在函数
在函数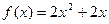 的图像上,其中
的图像上,其中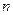 为正整数。
为正整数。 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列。
为等比数列。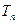 ,即
,即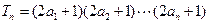 ,求数列
,求数列 ,求数列
,求数列 的前
的前 ,并求使
,并求使 的
的 ,函数
,函数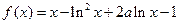
 .
.
 ,求
,求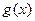 的最小值,并比较
的最小值,并比较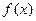 在
在 上是增函数;
上是增函数; 时,恒有
时,恒有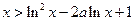 .
.
 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 胜利的概率;
胜利的概率;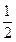 、
、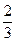 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.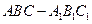 的底面边长为
的底面边长为
 ,侧棱
,侧棱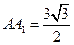 ,
, 是
是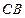 延长线上一点,且
延长线上一点,且

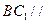 平面
平面 ;
; 的大小.
的大小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号