直线l与椭圆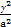
+
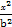=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=
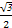,又椭圆经过点(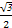,1),O为坐标原点.
(1)求椭圆的方程.
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
．
的最小正周期及对称中心；
，求
．
的值；
的值．
，
．
在
上的简图；
，
，求
．
．
，
．
与
的夹角的余弦值；
与
平行，求
的值．推荐套卷
直线l与椭圆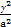+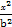=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=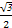,又椭圆经过点(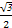,1),O为坐标原点.
(1)求椭圆的方程.
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
粤公网安备 44130202000953号