过点Q(-2,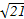
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
(1)求r的值.
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆O的切线l,且l交x轴于点A,交y轴于点B,设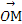
=
+
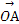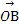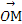,求||的最小值(O为坐标原点).
，
，
三点，这三点是否在同一条直线上，为什么？
，
，
，
是这条直线上的三个点，求
和
的值．
，
，
三点，试判断
的形状．
，
，
，
，试判断直线
与
的位置关系．相关知识点
推荐套卷
过点Q(-2,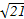)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
(1)求r的值.
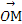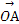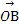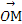(2)设P是圆O上位于第一象限内的任意一点,过点P作圆O的切线l,且l交x轴于点A,交y轴于点B,设=+,求||的最小值(O为坐标原点).
粤公网安备 44130202000953号