已知{an}是各项均为正数的等比数列,且a1+a2=2(
+
),a3+a4+a5=64(
+
+
),
(1)求{an}的通项公式.
(2)设bn=(an+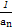
)2,求数列{bn}的前n项和Tn.
相关试题
＋
）n的展开式中，前三项的系数成等差数列，求展开式中的有理项．
，函数
的定义域为
且
，
当
时有
；
的值；
的单调区间．
.
；
,且最大边的边长为
，求最小边的边长.
有两个相等的实数根.
时，求
的值.相关知识点
推荐套卷
已知{an}是各项均为正数的等比数列,且a1+a2=2(+),a3+a4+a5=64(++),
(1)求{an}的通项公式.
(2)设bn=(an+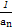)2,求数列{bn}的前n项和Tn.
粤公网安备 44130202000953号