已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为2,且当x=
时,f(x)的最大值为2.
(1)求f(x)的解析式.
(2)在闭区间[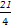
,
]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
相关知识点
推荐套卷
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为2,且当x=时,f(x)的最大值为2.
(1)求f(x)的解析式.
(2)在闭区间[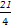,]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
粤公网安备 44130202000953号