已知函数f(x)＝ax＋x2，g(x)＝xln a，a>1.
(1)求证：函数F(x)＝f(x)－g(x)在(0，＋∞)上单调递增；
(2)若函数y＝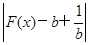
－3有四个零点，求b的取值范围；
(3)若对于任意的x1，x2∈[－1,1]时，都有|F(x2)－F(x1)|≤e2－2恒成立，求a的取值范围．
推荐套卷
已知函数f(x)＝ax＋x2，g(x)＝xln a，a>1.
(1)求证：函数F(x)＝f(x)－g(x)在(0，＋∞)上单调递增；
(2)若函数y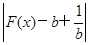＝－3有四个零点，求b的取值范围；
(3)若对于任意的x1，x2∈[－1,1]时，都有|F(x2)－F(x1)|≤e2－2恒成立，求a的取值范围．
粤公网安备 44130202000953号