已知直线y=x+6交x轴于点A,交y轴于点C,经过A和原点O的抛物线y=ax2+bx(a<0)的顶点B在直线AC上.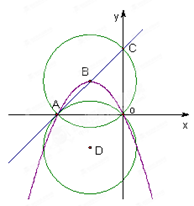
(1)求抛物线的函数关系式;
(2)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙B优弧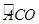 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
相关知识点
推荐套卷
已知直线y=x+6交x轴于点A,交y轴于点C,经过A和原点O的抛物线y=ax2+bx(a<0)的顶点B在直线AC上.
(1)求抛物线的函数关系式;
(2)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙B优弧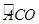 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.