已知双曲线x2－
＝1.
(1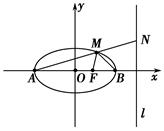)若一椭圆与该双曲线共焦点，且有一交点P(2,3)，求椭圆方程．
(2)设(1)中椭圆的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上的一动点，且在x轴上方，直线AN与椭圆交于点M.若AM＝MN，求∠AMB的余弦值；
(3)设过A、F、N三点的圆与y轴交于P、Q两点，当线段PQ的中点为(0,9)时，求这个圆的方程．
相关试题
在第一次抽取时被抽到的概率是多少?
推荐套卷
已知双曲线x2－＝1.
(1)若一椭圆与该双曲线共焦点，且有一交点P(2,3)，求椭圆方程．
(2)设(1)中椭圆的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上的一动点，且在x轴上方，直线AN与椭圆交于点M.若AM＝MN，求∠AMB的余弦值；
(3)设过A、F、N三点的圆与y轴交于P、Q两点，当线段PQ的中点为(0,9)时，求这个圆的方程．
粤公网安备 44130202000953号