某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛．若每盘比赛中高一、高二获胜的概率分别为
，
.
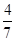(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？
(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望．
相关试题
为公差不为零的等差数列，首项
，
、
、 、
恰为等比数列，且
，
，
.
（用
表示）；
的前
项和为
, 求证：
（
的前
项和为
，
，若
成等比数列，且
时，
．
成等差数列；
的前n项和
．
｝的前n项和为Sn，公差d≠0，且S3=9，a1，a3，a7成等比数列．
＝
，求数列｛
.
中，
为常数，
，且
成公比不等于1的等比数列
的值；
，求数列
的前
项和
.
时，求函数
单调区间；
在区间[1,2]上的最小值为
,求
的值.推荐套卷
某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛．若每盘比赛中高一、高二获胜的概率分别为，.
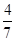(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？
(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望．
粤公网安备 44130202000953号