已知曲线C1的参数方程为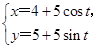
(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.
(1)把C1的参数方程化为极坐标方程；
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)．
相关试题
,其中向量
的最小正周期；
中, 
分别是角
的对边, 
求
的值.
是等边三角形，
是等腰直角三角形，
，
交
于
，
．
的值；
．
，
,
的夹角为60o, 
, 
,当实数
为何值时，⑴
∥
⑵
的前
项和为
，对任意的
，都有
，且
；数列
满足
.
的值及数列
的通项公式；
对一切
成立.推荐套卷
已知曲线C1的参数方程为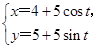(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.
(1)把C1的参数方程化为极坐标方程；
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)．
粤公网安备 44130202000953号