如图，点P(0，－1)是椭圆C1：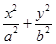
＝1(a>b>0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.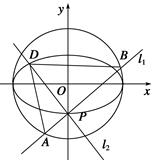
(1)求椭圆C1的方程；
(2)求△ABD面积取最大值时直线l1的方程．
相关试题
求证：
在（1，＋∞)上是增函数；
在
与
时都取得极值。
的值及函数
的单调区间；
恒成立，求
的取值范围。
上任意一点，曲线在M处的切线为
，求：（1）斜率最小的切线方程（2）切线
的取值范围。
中，
，设顶点
在底面
上的射影为
.
(2)求证：BC=DE
推荐套卷
如图，点P(0，－1)是椭圆C1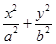：＝1(a>b>0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.
(1)求椭圆C1的方程；
(2)求△ABD面积取最大值时直线l1的方程．
粤公网安备 44130202000953号