(本大题满分12分)
某班级共有60名学生.先用抽签法从中抽取部分学生调查他们的学习情况,若每名学生被抽到的概率为 。
。
(I)求从中抽取的学生数,
(Ⅱ)若抽查结果如下表
| 每周学习时间(小时) |
 |
 |
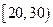 |
 |
| 人数 |
2 |
4 |
 |
1 |
先确定x,再完成频率分布直方图;
|
(III)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表)
相关知识点
推荐套卷
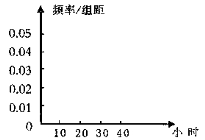

 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。 的最大值.
的最大值.
 的前n项和
的前n项和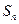 与通项
与通项 之间满足关系
之间满足关系
 求
求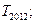
 ,求
,求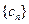 的前n项和
的前n项和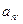
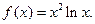
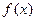 的单调区间;
的单调区间;
 ,在(1,2)上为单调递
,在(1,2)上为单调递 粤公网安备 44130202000953号
粤公网安备 44130202000953号