为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△内修建矩形水池,使顶点、在斜边上,、分别在直角边、上;又分别以、、为直径作半圆,它们交出两弯新月(图中阴影部分),两弯新月部分栽植花草;其余空地铺设地砖.其中 ,
, .设
.设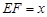 米,
米, 米.
米.
(1)求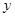 与
与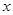 之间的函数解析式;
之间的函数解析式;
(2)当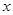 为何值时,矩形的面积最大?最大面积是多少?
为何值时,矩形的面积最大?最大面积是多少?
(3)求两弯新月(图中阴影部分)的面积,并求当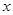 为何值时,矩形的面积等于两弯新月面积的
为何值时,矩形的面积等于两弯新月面积的 ?
?
相关知识点
推荐套卷

 ,
, 各表示几? 答:
各表示几? 答: _____ ,
_____ , _____;
_____;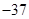
 ,
,
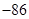

 ,0,
,0, ,
, ,
, ,
,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号