如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心．以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m．通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?（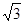
≈1．73）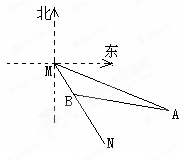
÷(x＋1)其中x＝
.
÷
，其中x＝
＋1.
÷
，其中x满足x2－x－1＝0.
＋1，y＝
的值．相关知识点
推荐套卷
如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心．以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m．通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?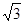（≈1．73）
粤公网安备 44130202000953号