已知双曲线x2-y2=2若直线n的斜率为2 ，直线n与双曲线相交于A、B两点，线段AB的中点为P，
(1)求点P的坐标（x,y)满足的方程（不要求写出变量的取值范围）；
(2)过双曲线的左焦点F1，作倾斜角为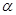
的直线m交双曲线于M、N两点，期中
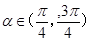，F2是双曲线的右焦点，求△F2MN的面积S关于倾斜角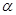的表达式。
相关试题
.
，求△ABC的周长L的取值范围.
，使得
的最大值为
，若存在，求出
,
在一个周期内，当
时，
取得最小值
；当
时，
，再将图像沿
轴向右平移
个单位，得到函数
的图像.
.
上的值域.相关知识点
推荐套卷
已知双曲线x2-y2=2若直线n的斜率为2 ，直线n与双曲线相交于A、B两点，线段AB的中点为P，
(1)求点P的坐标（x,y)满足的方程（不要求写出变量的取值范围）；
(2)过双曲线的左焦点F1，作倾斜角为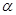的直线m交双曲线于M、N两点，期中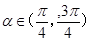，F2是双曲线的右焦点，求△F2MN的面积S关于倾斜角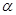的表达式。
粤公网安备 44130202000953号