在正三棱柱ABC-A1B1C1中，AB＝2，AA1＝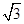
，点D为AC的中点，点E在线段AA1上．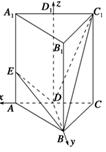
(1)当AE∶EA1＝1∶2时，求证DE⊥BC1；
(2)是否存在点E，使二面角D-BE-A等于60°，若存在求AE的长；若不存在，请说明理由．
的三个内角
成等差数列，求证：
均为实数，且
，
。
推荐套卷
在正三棱柱ABC-A1B1C1中，AB＝2，AA1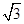＝，点D为AC的中点，点E在线段AA1上．
(1)当AE∶EA1＝1∶2时，求证DE⊥BC1；
(2)是否存在点E，使二面角D-BE-A等于60°，若存在求AE的长；若不存在，请说明理由．
粤公网安备 44130202000953号