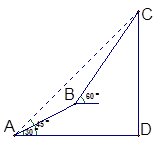
梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”N的仰角为45o,此时,他们刚好与峰底D在同一水平线上。然后沿着坡度为30o的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”N的仰角为60o,如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米,参考数据: )。
)。
相关知识点
推荐套卷
梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”N的仰角为45o,此时,他们刚好与峰底D在同一水平线上。然后沿着坡度为30o的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”N的仰角为60o,如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米,参考数据: )。
)。