在平面直角坐标系 中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D.
中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D.
(1)直接写出点B的坐标;
(2)如图,点P从点O出发,以每秒 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿 轴正方向移动.设移动时间为
轴正方向移动.设移动时间为 秒.
秒.
①当t为何值时,△OPQ的面积等于1;
②当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为y=- (x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
相关知识点
推荐套卷
 >0,
>0,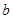 <0,且
<0,且 ,在数轴上表示
,在数轴上表示 , ―4, ―2
, ―4, ―2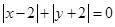 ,求
,求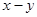 的相反数
的相反数 粤公网安备 44130202000953号
粤公网安备 44130202000953号