(1)第一盒乒乓球中有2个白球1个黄球,第二盒子乒乓球中有1个白球1个黄球,分别从每个盒中随机地取出1个球,求这两个球中欧一个是白球一个是黄球的概率;
解方程: ;
;
(3)如图,在⊙O中,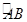 =
= ,∠A=30°,求∠B的度数
,∠A=30°,求∠B的度数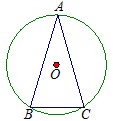
推荐套卷
(1)第一盒乒乓球中有2个白球1个黄球,第二盒子乒乓球中有1个白球1个黄球,分别从每个盒中随机地取出1个球,求这两个球中欧一个是白球一个是黄球的概率;
解方程: ;
;
(3)如图,在⊙O中,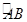 =
= ,∠A=30°,求∠B的度数
,∠A=30°,求∠B的度数