已知圆
：
，则下列命题：①圆上的点到
的最短距离的最小值为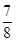
；②圆上有且只有一点
到点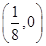
的距离与到直线
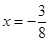的距离相等；③已知
，在圆上有且只有一点，使得以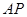
为直径的圆与直线
相切.真命题的个数为
A． |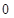
B． |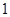
C． |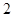
D． |
相关试题
在第三象限, 则角
的终边在( ).
的终边经过点
，则
的值是（）
，且
，则函数
（）
且
相关知识点
推荐套卷
已知圆：，则下列命题：①圆上的点到的最短距离的最小值为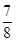；②圆上有且只有一点到点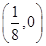的距离与到直线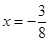的距离相等；③已知，在圆上有且只有一点，使得以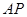为直径的圆与直线相切.真命题的个数为
| A． |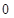
B． |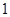
C． |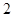
D． |
粤公网安备 44130202000953号