已知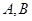 是抛物线
是抛物线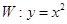 上的两个点,点
上的两个点,点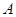 的坐标为
的坐标为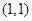 ,直线
,直线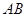 的斜率为
的斜率为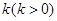 .设抛物线
.设抛物线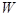 的焦点在直线
的焦点在直线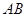 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且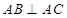 ,过
,过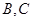 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为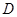 . 判断四边形
. 判断四边形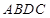 是否为梯形,并说明理由.
是否为梯形,并说明理由.
相关知识点
推荐套卷
已知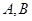 是抛物线
是抛物线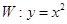 上的两个点,点
上的两个点,点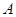 的坐标为
的坐标为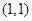 ,直线
,直线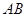 的斜率为
的斜率为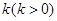 .设抛物线
.设抛物线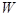 的焦点在直线
的焦点在直线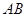 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且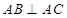 ,过
,过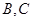 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为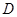 . 判断四边形
. 判断四边形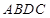 是否为梯形,并说明理由.
是否为梯形,并说明理由.