已知抛物线的解析式为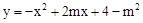
（1）求证：不论m为何值，此抛物线与x轴必有两个交点，且两交点A、B之间的距离为定值；
（2）设点P为此抛物线上一点，若△PAB的面积为8，求符合条件的点P的坐标；
（3）若（2）中△PAB的面积为S（S>0），试根据面积S值的变化情况，确定符合条件的点P的个数（本小题直接写出结论，不要求写出计算、证明过程）.
,则
）=1*
.
，y2
，当x为何值时，y1与y2互为相反数?
相关知识点
推荐套卷
已知抛物线的解析式为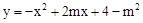
（1）求证：不论m为何值，此抛物线与x轴必有两个交点，且两交点A、B之间的距离为定值；
（2）设点P为此抛物线上一点，若△PAB的面积为8，求符合条件的点P的坐标；
（3）若（2）中△PAB的面积为S（S>0），试根据面积S值的变化情况，确定符合条件的点P的个数（本小题直接写出结论，不要求写出计算、证明过程）.
粤公网安备 44130202000953号