如图,已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16海里,一艘货轮从B港口以40海里/h的速度沿∠ABC=45°的BC方向航行.现测得C处位于A观测点北偏东79.8°(即∠DAC=79.8°)方向.求此时货轮C与AB之间的最近距离(精确到0.1海里).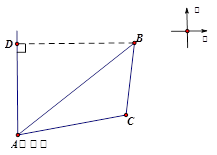
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,)
相关知识点
推荐套卷
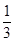 ×[2—(—3)2];
×[2—(—3)2];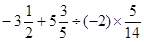 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号