已知函数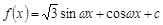
（
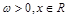，c是实数常数）的图像上的一个最高点
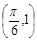，与该最高点最近的一个最低点是
，
(1)求函数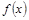
的解析式及其单调增区间；
(2)在△ABC中，角A、B、C所对的边分别为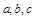
，且
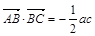，角A的取值范围是区间M，当
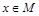时，试求函数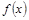的取值范围.
，求证：
不能同时大于
．
为等差数列，公差
，数列
满足
．判断数列
，
，
，至少有一个方程有实根，试求实数
的取值范围．
对任意
，都有
且
时，
．
上为减函数．
焦点的弦为直径的圆必与
相切（用分析法证）推荐套卷
已知函数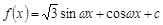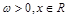（，c是实数常数）的图像上的一个最高点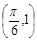，与该最高点最近的一个最低点是，
(1)求函数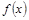的解析式及其单调增区间；
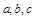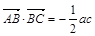(2)在△ABC中，角A、B、C所对的边分别为，且，角A的取值范围是区间M，当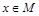时，试求函数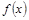的取值范围.
粤公网安备 44130202000953号