椭圆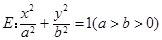
与双曲线
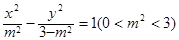有公共的焦点，过椭圆E的右顶点作任意直线l，设直线l交抛物线
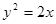于M、N两点，且
．
(1)求椭圆E的方程；
(2)设P是椭圆E上第一象限内的点，点P关于原点O的对称点为A、关于x轴的对称点为Q，线段PQ与x轴相交于点C，点D为CQ的中点，若直线AD与椭圆E的另一个交点为B，试判断直线PA，PB是否相互垂直？并证明你的结论．
相关试题
（c是常数，
）且
成公比不为1的等比数列。
的通项公式。
满足：
，
.
.
及
（
）,求数列
的前n项和
.
中，
的离心率
，过点
和
的直线与原点的距离为
.
与该双曲线交于不同的两点
，且
为圆心的同一圆上，求
的取值范围.
中，底面
是矩形，
平面
，
，
、
分别是
、
的中点.
平面
；
夹角的大小.
相关知识点
推荐套卷
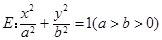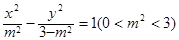椭圆与双曲线有公共的焦点，过椭圆E的右顶点作任意直线l，设直线l交抛物线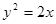于M、N两点，且．
(1)求椭圆E的方程；
(2)设P是椭圆E上第一象限内的点，点P关于原点O的对称点为A、关于x轴的对称点为Q，线段PQ与x轴相交于点C，点D为CQ的中点，若直线AD与椭圆E的另一个交点为B，试判断直线PA，PB是否相互垂直？并证明你的结论．
粤公网安备 44130202000953号