如图,AB是⊙O的直径,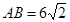 ,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.
,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.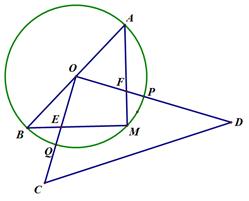
(1)求证: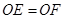 ;
;
(2)连接PM、QM,试探究:在△COD绕点O旋转的过程中,∠PMQ是否为定值?若是,求出∠PMQ的大小;若不是,请说明理由;
(3)连接EF,试探究:在△COD绕点O旋转的过程中,△EFM的周长是否存在最小值?若存在,求出其最小值;若不存在,请说明理由
相关知识点
推荐套卷
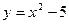 ,且y的算术平方根是2,求
,且y的算术平方根是2,求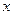 的值。
的值。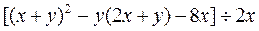 ,其中
,其中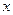 =-2 .
=-2 .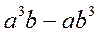 (2)
(2)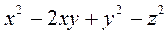
 粤公网安备 44130202000953号
粤公网安备 44130202000953号