一场篮球赛中,小明跳起投篮,已知球出手时离地面高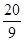
米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,若篮球运行的轨迹为抛物线,篮圈中心距离地面3米.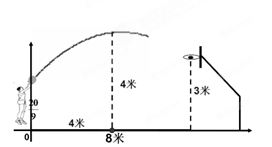
（1）建立如图的平面直角坐标系,求抛物线的解析式；
（2）问此球能否投中？
的三边长分别为
,
,
.若将
折叠，点
正好落在
边上的点
处.求线段
的长度.
中，
，
cm，正方形
的面积为
cm2，
于点
，求
的长.
，其中
，
.
相关知识点
推荐套卷
一场篮球赛中,小明跳起投篮,已知球出手时离地面高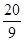米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,若篮球运行的轨迹为抛物线,篮圈中心距离地面3米.
（1）建立如图的平面直角坐标系,求抛物线的解析式；
（2）问此球能否投中？
粤公网安备 44130202000953号