许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称.经过测算,中间抛物线的解析式为:y=-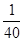 x2+10,并且BD=
x2+10,并且BD=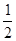 CD.
CD.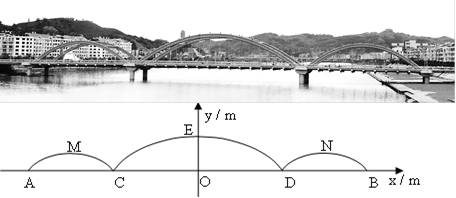
(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式.
相关知识点
推荐套卷
许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称.经过测算,中间抛物线的解析式为:y=-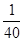 x2+10,并且BD=
x2+10,并且BD=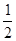 CD.
CD.
(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式.