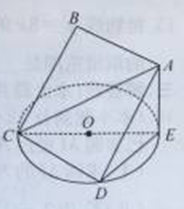
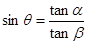如图,正方形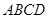 所在平面与圆
所在平面与圆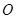 所在的平面相交于
所在的平面相交于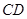 ,线段
,线段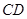 为圆
为圆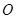 的弦,
的弦,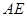 垂直于圆
垂直于圆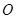 所在的平面,垂足
所在的平面,垂足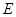 为圆
为圆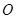 上异于
上异于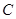 、
、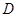 的点,设正方形
的点,设正方形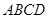 的边长为
的边长为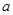 ,且
,且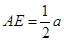 .
.
(1)求证:平面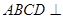 平面
平面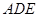 ;
;
(2)若异面直线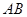 与
与 所成的角为
所成的角为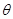 ,
,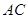 与底面
与底面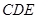 所成角为
所成角为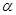 ,二面角
,二面角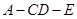 所成角为
所成角为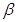 ,求证
,求证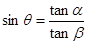
相关知识点
推荐套卷
如图,正方形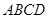 所在平面与圆
所在平面与圆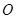 所在的平面相交于
所在的平面相交于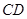 ,线段
,线段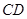 为圆
为圆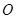 的弦,
的弦,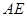 垂直于圆
垂直于圆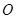 所在的平面,垂足
所在的平面,垂足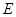 为圆
为圆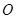 上异于
上异于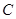 、
、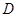 的点,设正方形
的点,设正方形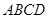 的边长为
的边长为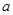 ,且
,且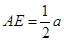 .
.
(1)求证:平面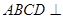 平面
平面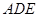 ;
;
(2)若异面直线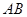 与
与 所成的角为
所成的角为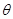 ,
,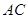 与底面
与底面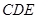 所成角为
所成角为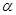 ,二面角
,二面角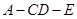 所成角为
所成角为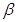 ,求证
,求证