先阅读，后解答：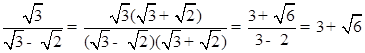
像上述解题过程中，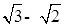
与
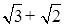相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化，
（1）
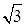的有理化因式是 ； 
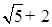的有理化因式是 ．
（2）将下列式子进行分母有理化：
（1）
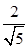= ；（2）
= ．
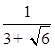（3）已知a=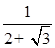
,b=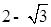
，比较a与b的大小关系．
的解是x = 4，求
的值
y
中x=－3，y=2
、点
分别在
的边上，请根据下列语句画出图形：
；
与
相交于点
；
的中点
，连接
.相关知识点
推荐套卷
先阅读，后解答：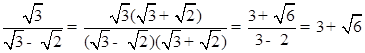
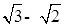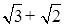像上述解题过程中，与相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化，
（1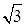）的有理化因式是 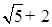； 的有理化因式是 ．
（2）将下列式子进行分母有理化：
（1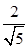）= ；（2）= ．
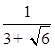（3）已知a=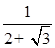,b=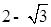，比较a与b的大小关系．
粤公网安备 44130202000953号