如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上．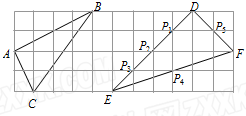
（1）判断△ABC和△DEF是否相似，并说明理由；
（2）P1，P2，P3，P4，P5，D，F是△DEF边上的7个格点，请在这7个格点中选取3个点作为三角形的顶点，使构成的三角形与△ABC相似（要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由）．
b）
+8（a
km，冥王星和太阳的平均距离约是水星和太阳的平均距离的102倍，那么冥王星和太阳的平均距离约为多少km？
次运算，它工作5×10
秒可作多少次运算？
·a
-2a
·a
-3a
·a
.
·（2x-y）·（2x-y）
；相关知识点
推荐套卷
如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上．
（1）判断△ABC和△DEF是否相似，并说明理由；
（2）P1，P2，P3，P4，P5，D，F是△DEF边上的7个格点，请在这7个格点中选取3个点作为三角形的顶点，使构成的三角形与△ABC相似（要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由）．
粤公网安备 44130202000953号