小莉的爸爸买了今某演唱会的一张门票,她和哥哥两人都很想去观看,可门票只
有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字
为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,
然后将抽出的两张牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平吗?为什么?若不公平,请设计一种公平的游戏规则.
相关知识点
推荐套卷

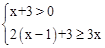 ,并判断﹣1、
,并判断﹣1、 这两个数是否为该不等式组的解.
这两个数是否为该不等式组的解. x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.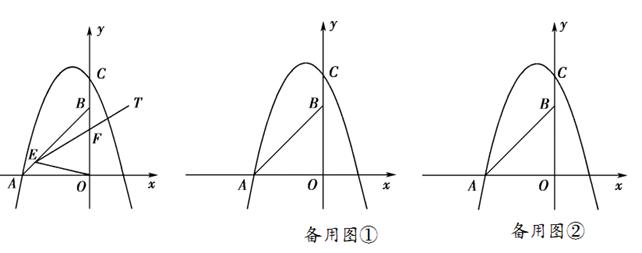
 ) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由. ,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.
,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.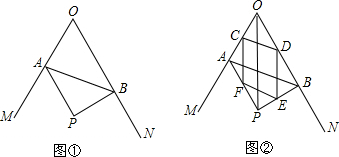
 粤公网安备 44130202000953号
粤公网安备 44130202000953号