某工厂甲、乙两个车间包装同一种产品，在自动包装传送带上每隔
小时抽一包产品，称其重量（单位：克）是否合格，分别记录抽查数据，获得重量数据的茎叶图如图所示.
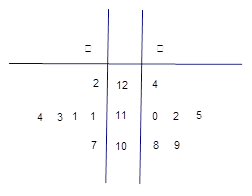
（1）根据样品数据，计算甲、乙两个车间产品重量的平均值与方差，并说明哪个车间的产品的重量相对较稳定；
（2）若从乙车间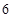
件样品中随机抽取两件，求所抽取的两件样品的重量之差不超过
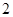克的概率.
相关试题
，并在点C测得塔顶A的仰角为
，求塔高AB.
的最小正周期;
的值．
的单调增区间
为锐角，
，求
的值．
>0为常数，若
上是增函数，求
若A
B恒成立，求实数
的取值范围．
，
，
．
，求角A的值．推荐套卷
某工厂甲、乙两个车间包装同一种产品，在自动包装传送带上每隔小时抽一包产品，称其重量（单位：克）是否合格，分别记录抽查数据，获得重量数据的茎叶图如图所示.
（1）根据样品数据，计算甲、乙两个车间产品重量的平均值与方差，并说明哪个车间的产品的重量相对较稳定；
（2）若从乙车间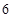件样品中随机抽取两件，求所抽取的两件样品的重量之差不超过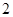克的概率.
粤公网安备 44130202000953号