某公司承担了每天至少搬运280吨水泥的任务，已知该公司有6辆A型卡车和8辆B型卡车．又已知A型卡车每天每辆的运载量为30吨，成本费为0.9千元；B型卡车每天每辆的运载量为40吨，成本费为1千元．
（1）如果你是公司的经理，为使公司所花的成本费最小，每天应派出A型卡车、B型卡车各多少辆？
（2）在（1）的所求区域内，求目标函数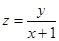
的最大值和最小值.
相关试题
，b＝4，且BC边上的高h＝
。
，若不等式
恒成立，求实数
的取值范围.
（
为参数）被曲线
所截的弦长.
，过顶点
的圆与边
切于
，与边
分别交于点
，且
，点
平分
.求证：
.
、
是函数
的两个极值点。
，求函数
的解析式；
，求
的最大值。推荐套卷
某公司承担了每天至少搬运280吨水泥的任务，已知该公司有6辆A型卡车和8辆B型卡车．又已知A型卡车每天每辆的运载量为30吨，成本费为0.9千元；B型卡车每天每辆的运载量为40吨，成本费为1千元．
（1）如果你是公司的经理，为使公司所花的成本费最小，每天应派出A型卡车、B型卡车各多少辆？
（2）在（1）的所求区域内，求目标函数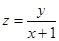的最大值和最小值.
粤公网安备 44130202000953号