如图，抛物线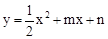
与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.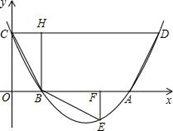
（1）求C点的坐标及抛物线的解析式；
（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
（3）设过点E的直线交AB边于点P，交CD边于点Q.问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.
相关试题
如图，把一个矩形纸片ABCD沿AD和BC的中点连线EF对折，要使矩形AEFB与原矩形相似，且AB=6.
（1) 求AD的长。
（2）求矩形AEFB与原矩形ABCD的相似比。
八年级（1）班的学生周末乘汽车到游览区游览，游览区距学校120km，一部分学生乘慢车先行，出发1h后，另一部分学生乘快车前往，结果他们同时到达游览区，。已知快车的速度是慢车速度的1.5倍，求慢车的速度。
；其中：x="2"
≤1
相关知识点
推荐套卷
粤公网安备 44130202000953号