如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园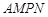 ,要求:B在
,要求:B在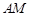 上,D在
上,D在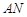 上,对角线
上,对角线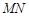 过C点,且矩形
过C点,且矩形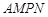 的面积小于64平方米.
的面积小于64平方米.
(Ⅰ)设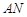 长为
长为 米,矩形
米,矩形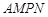 的面积为
的面积为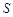 平方米,试用解析式将
平方米,试用解析式将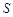 表示成
表示成 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当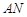 的长度是多少时,矩形
的长度是多少时,矩形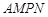 的面积最小?并求最小面积.
的面积最小?并求最小面积.
推荐套卷
如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园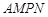 ,要求:B在
,要求:B在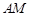 上,D在
上,D在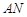 上,对角线
上,对角线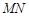 过C点,且矩形
过C点,且矩形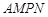 的面积小于64平方米.
的面积小于64平方米.
(Ⅰ)设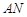 长为
长为 米,矩形
米,矩形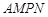 的面积为
的面积为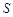 平方米,试用解析式将
平方米,试用解析式将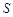 表示成
表示成 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当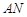 的长度是多少时,矩形
的长度是多少时,矩形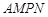 的面积最小?并求最小面积.
的面积最小?并求最小面积.