已知曲线
的参数方程是
(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程是ρ＝2，正方形ABCD的顶点都在上，且A，B，C，D依逆时针次序排列，点A的极坐标为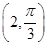
.
（Ⅰ）求点A，B，C，D的直角坐标；
（Ⅱ）设P为上任意一点，求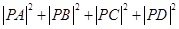
的取值范围．
在
和
附近的平均变化率，并比较它们的大小.
，过原点且倾斜角为
的两条直线分别交椭圆于A、C和B、D两点．（1）用
表示四边形ABCD的面积S；（2）当
时，求S的最大值．
相交于A、B两点，当t变化时，求|AB|的最大值．
的椭圆的中心的轨迹方程
为参数）的准线方程相关知识点
推荐套卷
已知曲线的参数方程是 (φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线的极坐标方程是ρ＝2，正方形ABCD的顶点都在上，且A，B，C，D依逆时针次序排列，点A的极坐标为.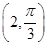
（Ⅰ）求点A，B，C，D的直角坐标；
（Ⅱ）设P为上任意一点，求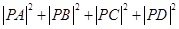的取值范围．
粤公网安备 44130202000953号